Coaxial Cable Impedance Calculator

The dominant use of coaxial cable in RF & Microwave applications is as a transmission line. Coaxial cables are extremely useful transmission lines as the coaxial nature of the transmission line provides relatively efficient transmission from DC to a cut-off frequency, which is a function of the geometries of the coaxial components of the cable.

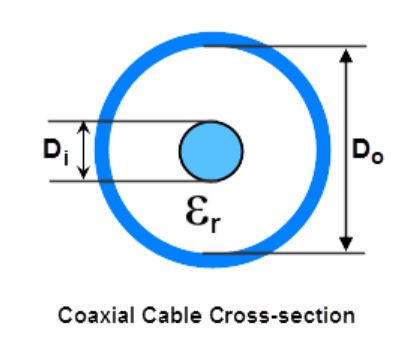
coax cross section

It is also relatively straightforward to calculate the inductance per unit length, capacitance per unit length, characteristic impedance, and velocity of propagation with only knowing a few basic characteristics of the inner conductor, outer conductor, and dielectric material between the coaxial conductors. It is important to note that these calculations are based on the assumption that the inner and outer conductor are truly coaxial and there is a reasonably tight tolerance of the material geometries along the cable, otherwise these values will be different for every segment of the coaxial cable that are not conformal.

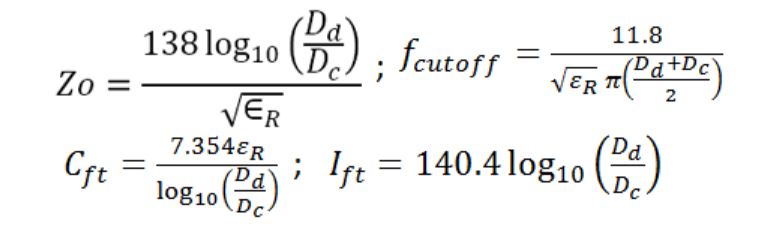
characteristic impedance formula

The equations above can be used to calculate the characteristic impedance, cut-off frequency, capacitance per unit length, and inductance per unit length. What is needed is the outer diameter of the inner conductor (Dc), the inner diameter of the outer conductor (Dd), and the relative permittivity of the dielectric separating the inner and outer conductors. The inner conductor outer diameter is also the dielectric inner diameter, and the outer conductor inner diameter is also the dielectric outer diameter. Using a constant that is derived by the permittivity of free space, the speed of light, and the magnetic permeability of free space, it is possible to calculate for each of the parameters previously mentioned.

The result is a characteristic impedance in Ohms (Z0), the cut-off frequency (f_cutoff) in Hz, the capacitance per unit length (Cft) in farads, and the inductance per unit foot in Henrys. It is also possible to solve for the velocity of propagation, which is simply a percentage of the speed of light derived from one divided by the square root of the permittivity of the dielectric. This is because the primary mode in a coaxial transmission line is the transverse electromagnetic (TEM) mode where the poynting vector of the field is in line with the coaxial conductors and passes through the dielectric. The closer the dielectric is to air, the higher the velocity of propagation is and the closer it is to the speed of light in vacuum.

In case these calculations seem burdensome, Pasternack provides a free-to-use Coaxial Cable Impedance Calculator online here: https://www.pasternack.com/t-calculator-coax-cutoff.aspx. All that is needed is for the user to input the dielectric inner and outer diameters, select the units used for these measurements, and finally input the dielectric constant (relative permittivity) of the dielectric. The calculator will output the characteristic impedance, cut-off frequency, capacitance per unit length, inductance per unit length, and velocity of propagation in percentage of the speed of light.